Half Donut Chart in Tableau

I am regularly asked how to create a half-donut chart in Tableau, kind of like this:

 

 

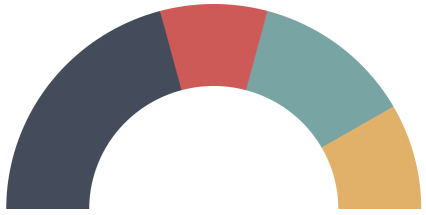
My first response is always to recommend another chart, partially because there is typically a better chart that is easier to understand and takes up less space, but also because it’s really hard to build in Tableau. Others have addressed the first part of this concern, so I’m not going to spend time on it here. Rather, I want to focus on what makes this chart so difficult to build in Tableau (don’t worry—I’ll provide a method for creating this chart at the end of the blog).

 

Haven’t You Done This Before?

When I tell people that this is very difficult to build, they are often confused. After all, I’ve created NPS Gauges

 

 

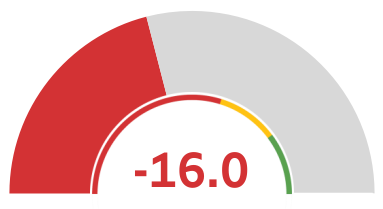
…and Percentage Gauges

 

 

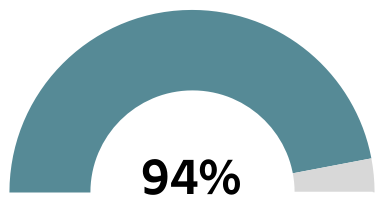
Plus, regular donuts charts are easy to create in Tableau. So, why would a half donut chart be so difficult? Well, let’s walk through it. We’ll start by creating a donut chart using the following data.

 

 

This can be done pretty easily through use of a dual axis chart—one axis using a pie chart and one using a circle mark (to create the donut hole).

 

 

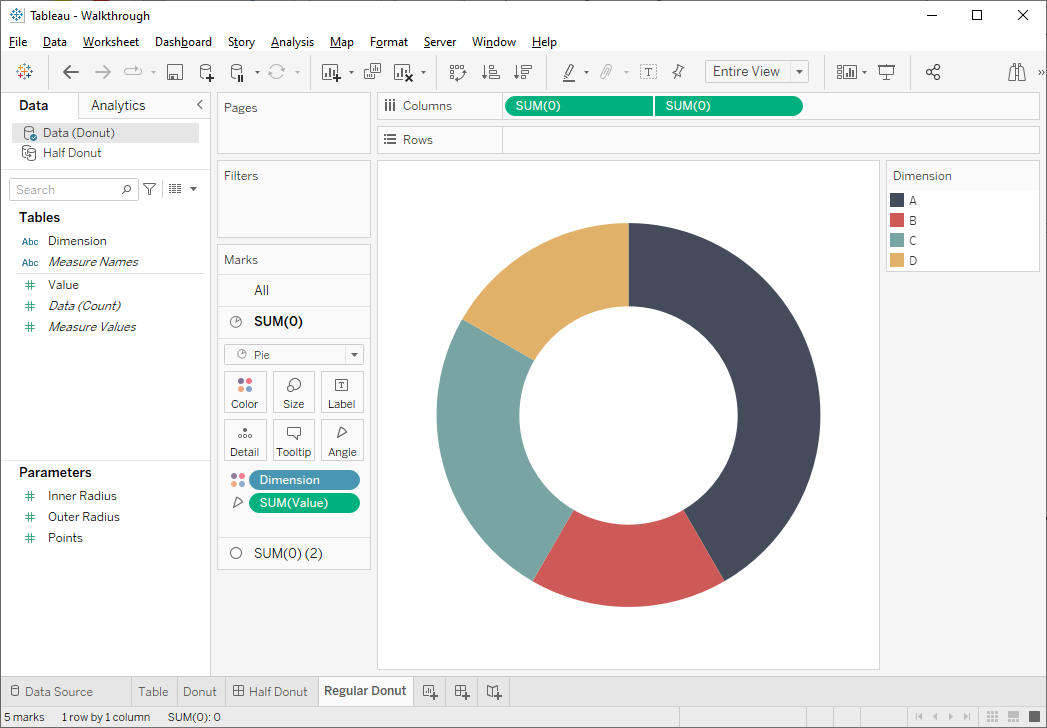
Note the position of Dimension A. Since this field is sorted alphabetically, it’s the first dimension that is plotted and it starts at the 12:00 point, then moves clockwise. The first dimension is always plotted in this way. But starting at that 12:00 point makes no sense with a half donut chart. Instead, we want to start at the 9:00 point and move clockwise. If Tableau allowed us to rotate the pie chart, then we could easily do that, but that’s not an option—we can only start that first segment at 12:00.

 

This brings me to the NPS and Percentage Gauges I’ve previously created. If the above is a problem, how did I create these? Well, this was a big challenge as we have to identify which segment crosses the 12:00 point, then split it up into two segments—one to the right of the 12:00 point (our very first segment) and one to the left (our final segment). My approach was to create a donut chart with 5 pre-defined slices, as shown below.

 

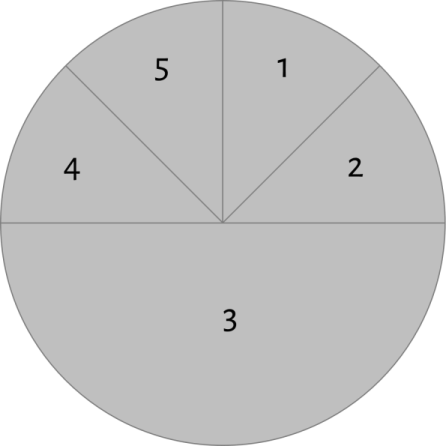
This allows us to start at 12:00 and draw our slices clockwise. But it requires a bit of math to determine the size and color of each of the slices. This is doable because my NPS and Percentage Gauges only visualize one number—an NPS value or a Percentage. Because of this, the chart really only has two segments. The first is colored and shows the value, while the second is grey and shows what’s left. So, using the five-slice technique, we need to determine which of the two segments crosses that 12:00 mark. Based on that, we can break up the four slices needed to create the chart (slice 3 is always the same size and matches the background color so that it looks invisible). The logic for this is a bit tricky and requires a fair number of calculated fields, but it’s doable.

 

But what happens when we need to visualize a variable number of segments as with a half donut? Unfortunately, in this case, the logic becomes exponentially more complex, requires more than five slices, and involves the use of running sums to determine the cut-off mark. Would this be possible? Maybe, but it would be really difficult.

 

At this point, we should be asking if the juice is worth the squeeze. In almost every case, I’d say no—this chart isn’t so special that it’s worth going through all this pain to create it. In most cases, a simple donut chart, pie chart, or something else entirely would suffice.

 

A Method for Creating Half Donuts

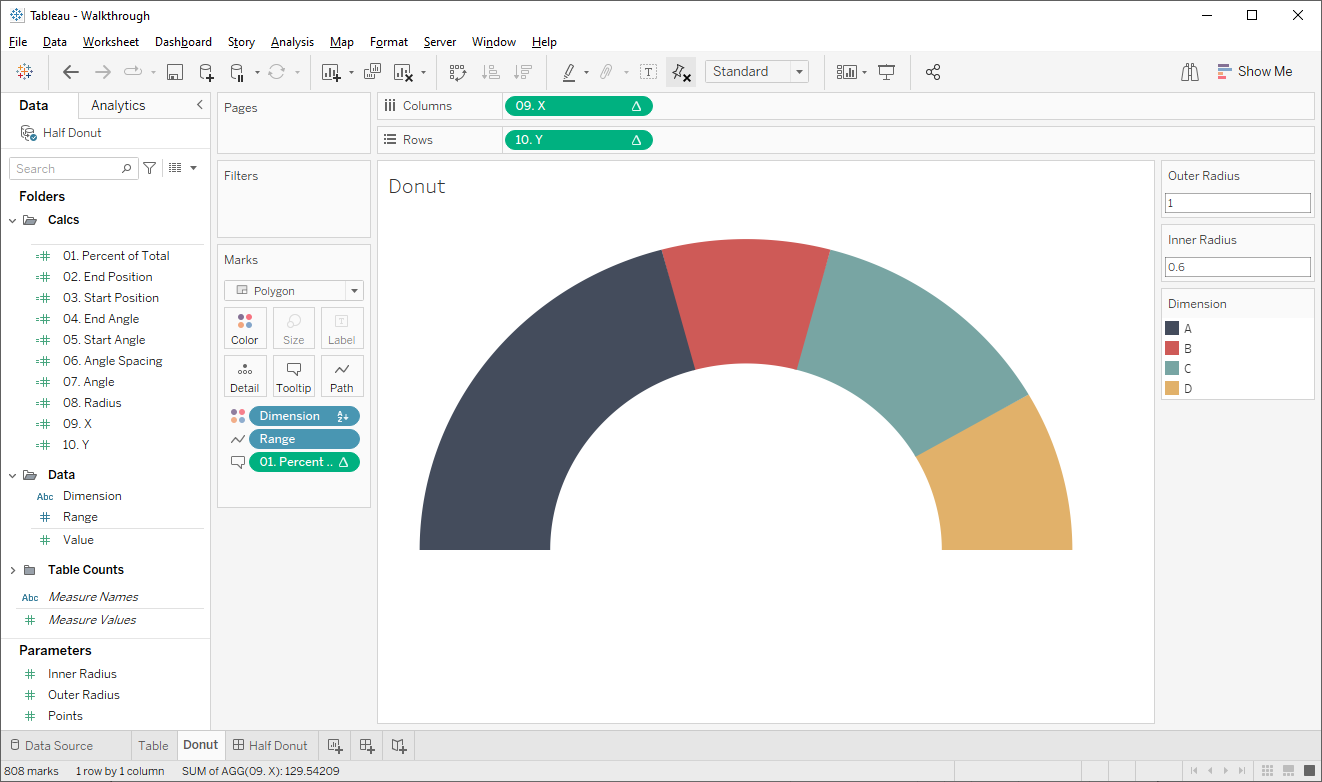
You didn’t think I’d title this blog, Half Donut Chart in Tableau, then just leave it at “don’t do it!”, did you? 😉 As I’ve said before, there’s almost nothing you can’t create in Tableau. Unfortunately, due to what I’ve already explained, pie charts don’t seem like a viable option for this type of chart. So, instead, I’ll be leveraging polygons. We’ll have to first densify our data so we can draw the curves using trigonometry. We’ll do the following using calculated fields:

 

1) Determine the proportion of the total for each segment.

2) Use running sums to find the start and end point of each segment.

3) Translate the start and end point into angles ranging from 0° (3:00) to 180° (9:00).

4) Using the densification points and trigonometry calculate the X and Y coordinates around the outer curve of each segment then connect it to the inner edge then draw that to complete each polygon.

 

In the end, we’re able to produce the chart:

 

 

Feel free to download the workbook if you’d like to take a closer look at the calculations.

 

As you can see, this isn’t easy…and yet, I still felt like this was easier than trying to figure out the pie chart logic. That tells you something! Once again, I’d ask if the the juice is worth the squeeze?

 

Using the Template

Okay, so maybe you’ve read all this, understand why it’s difficult and you still want to use this chart type in your project. Fortunately, I’ve templatized this to make it as easy as possible.

 

Like our other templates, this one includes two components—an Excel spreadsheet and a Tableau workbook. The Excel spreadsheet has two sheets, Data and Model. Model is used to handle the data densification needed to draw the curves. You don’t need to worry too much about this sheet—just make sure it’s in your spreadsheet. Data is used to populate your data. It contains two columns, Dimension and Value. Dimension defines the individual segments of the donut while Value is used to determine the size of each segment. If you’d like to add new columns, that’s fine—just make sure you have Dimension and Value.

 

Next download the Tableau template. Edit the data source and connect it to your Excel file. The workbook should update automatically to reflect your data.

 

If you’d like to adjust the thickness of the donut, you can change the Inner Radius parameter. Values closer to 1 will create a thinner donut, while values closer to 0 will create a thicker one.

 

Wrap-Up

As I’ve said numerous times already, if you’re considering creating a half-donut chart, take a moment to think about whether or not it’s really the best option. This type of chart has a number of problems and is also very difficult to create. That said, like everything, there’s always an exception to the rule and there are times when this might be the perfect chart. Just know that it’s not as straightforward as a regular donut chart or even a gauge chart. If, after reading all this, you still want to create it, feel free to leverage my template. Thanks for reading! If you have any questions or comments, please let me know in the comments.

 

Ken Flerlage, December 11, 2022

Hire Us! | Twitter | LinkedIn | GitHub | Tableau Public